Découvrir la Notation Big O

La notation Big O ou comment mesurer le complexité  temporel et spatial d’un algorithme

Quel titre! Ne vous inquiétez pas, vous gérez.

D’abord, O(N) se lit O de N.

Big O est un concept très important à comprendre, je crois que quelqu’un ne peut pas travailler chez google ou Microsoft en tant que développeur sans le connaitre. Ce concept fait souvent le premier filtre aux entretiens et pourtant votre collègue peut vous dire qu’il n’a jamais utilisé pendant ses vingtaines d’années d’expérience. Il a tort et google et Microsoft ont raison.

Voici comment maîtriser ce concept qui est en effet facile à comprendre. Ce n’est qu’une valeur ajoutée pour votre entretien.

Partons avec un exemple de mon bouquin favori. Supposons que j’ai un fichier et je veux le transférer à mon ami à Istanbul. Quelle est la meilleure méthode pour le faire?

1- Télécharger par internet

2- Prendre le fichier avec moi sur un avion et faire le trajet Paris-Istanbul? (Pour les radins on va supposer que le prix de billet n’est pas important)

Eh bien, mesdames et messieurs, ça dépend de la taille du fichier!

Pour un fichier de taille raisonnable, nous avons internet à notre service.

Pour un fichier de 1to vaut mieux faire le trajet de 7h ( 3h30 de vol plus transport et attente dans l’aéroport). Voici un joli graph pour le voir autrement: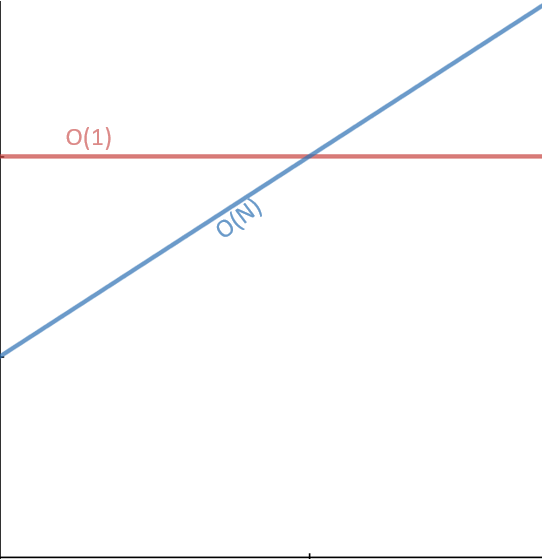

Graph 1 :

Méthode Istanbul: Le temps d’exécution est constant: O(1), il est indépendant de la taille de fichier.

Méthode transfère sur internet: On peut supposer que le temps d’exécution est linéaire, plus la taille est grande plus longue que ça va durer:  O(N)

Peu importe le constant , un moment donné linéaire devrait  dépasser le constant.

Et voilà; ça c’est complexité temporel  ou asymptotic runtime en anglais  ou Big O runtimeS.  Comment je peux exprimer l’évolution de temps d’exécution en fonction de mes input. Dans notre cas: en fonction de la taille du fichier.

Donc c’est une question de mesurer le  “scalability” de mon algorithme:
Scalability(en) ==  Evolutivité (fr)

Il y a d’autre Big O qu’on voit souvent à part O(N) et O(1) qu’on vient de voir, par ex:  O(log N), O (NlogN), O(N²), O(2^N).

 

Complexité Spatial

Après le complexité temporel, il y a le complexité spatial, qui pose la question : comment ma mémoire évolue ? Supposons que je veux créer un tableau de n éléments, alors j’ai besoin de O(n) d’espace dans la mémoire. Si un tableau de n*n (une matrice de n*n) , j’ai besoin de O(n²) d’espace.

Si simple que ça !

 

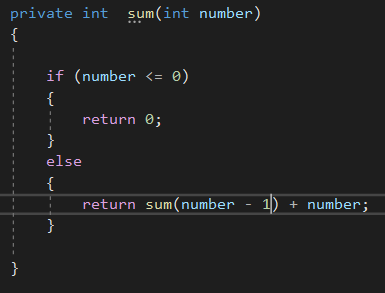
Voyons cette méthode. Elle va avoir un temps d’execution O(N) et va occuper O(N) espace.

Car chaque fois il y aura une méthode dans le tas ( stack en anglais)

Par ex: sum(5) va appeler sum(4)…

=> sum (4)

=>sum (3)

=> sum(2)

=>sum (1)

=>sum(0)

 

Alors à partir de là le stack peut “se libérer”… En fonction d’espace qu’on occupe, on peut dire que c’est complexité spatial de O(n). Petite note, des fois sur coding game, vous recevrez un message : votre algorithme n’est pas optimal. Autant que nous sommes libre d’écrire une méthode pour la suite fibonacci en récursive, à partir d’un certain nombre, nous allons surement peter le tas. Stack over flow exception.

 

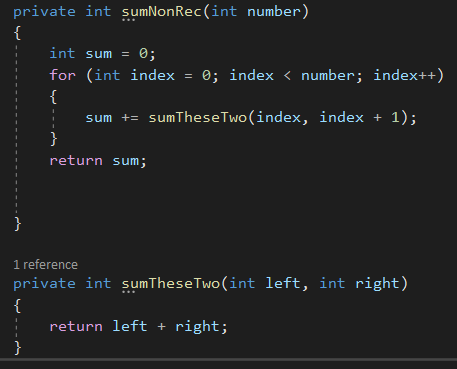
2ème méthode aussi fait n appels, par contre les appels ne sont pas tous sur le tas en même temps. Donc c’est de O(n) de temps et O(1) d’espace.

Clés de réussite dans un entretien pour Big O

Petit rappel : O(1) veut dire constant. Ca peut être 70 ou 3, on s’en fou.

Un code O(N) peut donc s’exécuter plus rapide que O(1) pour des inputs spécifique. Pour cette raison, on ignore les constants devant N.

Clé 1: Ignorer les constants devant N.

Ne dites jamais O(2N) dans un entretien!!! C’est O(N).

Beaucoup de gens résistent à faire ça, ils voient deux boucles for consécutifs et ils disent O(2N). Ils croient être précis, mais, non. Ce n’est pas plus précis. Big O nous permet d’exprimer comment le temps d’exécution évolue.

Clé 2: Ignorer l’expression négligeable.
Ne dites jamais O(N² +N ) dans un entretien. C’est O(N²)

Voici comment on y arrive:

On a déjà dit qu’on néglige les constants. Donc O(2N²) = O(N² +N²) devient O(N²) .

On vient de négliger N².
Or comme N² > N, on va bien sur ignorer N.
O(N²+N) devient O(N²).

Quelques exemples :

1) O(N +logN) devient O(N)

2) O(5 *2^N + 1000 N¹⁰⁰) devient O(2^N)

Attention si on se trouve avec une somme : O(B² + A) on devrait connaitre les valeurs de B et A pour décider l’expression finale. Voir l’exemple dans clé 3:

Clé 3: Somme vs Multiplication

Si mon algo dit fait ça ensuite quand tu finis, fait cela, je fais  la somme. Complexité : O(A+B ). Rappel: A et B inconnu, alors on garde, on néglige rien.

 

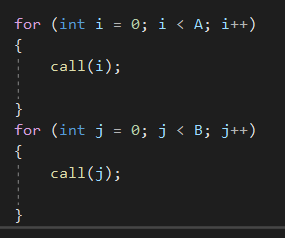
Si mon algo dit fait cela et pour chaque fois fait ça, je multiplie. Complexité : O(A*B)

 

Voici un autre joli graph des temps Big O que nous voyons souvent :

 

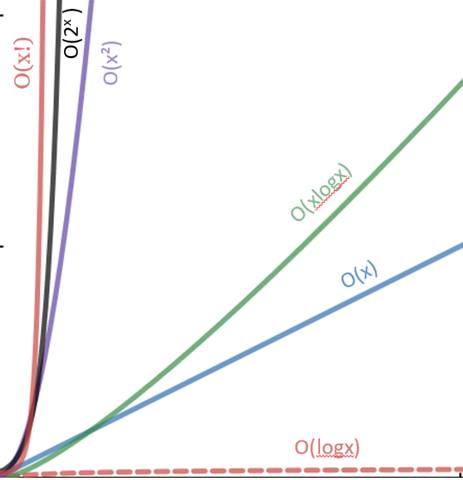
O(x²) est pire que O(xlogX) mais pas aussi pire que O(x!)

 

Le temps amorti

Soit Un ArrayList est un tableau dynamique qui ne nécessite pas d’être instancié avec une taille. On l’implémente avec un tableau d’une taille fixe et on multiplie par deux la taille au fur est au mesure que nous avons besoin des places supplémentaires.

Comment calculer le temps d’exécution ( Big O ) d’une insertion?

C’est un peu compliqué car il y a plusieurs cas: Si c’est plein, avec N éléments, je dois doubler la taille, et copier N éléments: Dans le cas plein, C’est O(N).

Mais souvent ce n’est pas plein, donc je ne copie pas N éléments: Dans ce cas c’est constant, c’est O(1).

On a besoin d’un concept qui  prend compte de ces deux cas: Le pire de cas arrive, mais ça arrive si rarement que nous disons que le temps est amorti.

 

Calculons dans  notre cas le temps amorti:
Supposons que j’ai un arraylist avec 1 élément, si je veux ajouter un élément, il faudrait changer la taille à deux, ensuite copier l’élément existant et insérer le nouveau. Si je voudrais encore ajouter une valeur, la taille est encore multiplié par deux, cette fois je copie les deux éléments, j’insère le troisième. Pour la quatrième élément, j’ai encore une place, je n’ai pas besoin de multiplier par deux la taille, ni copier, j’insère simplement.

Donc je fais l’opération de copie que quand le tableau est pleine: 1,2,4,8,16,32,…. N donc si je fais N insertions, je fais 1,2,4,8,16,32,…. N copies respectivement.

(A ce stade je vous propose de faire le dessin de ce qui se passe pour les 5 premier cas, pour faciliter la compréhension, si je ne suis pas assez claire…)

Donc pour N insertions j’ai N + N/2+ N/4+…..+1 copies.
La somme fait à peine 2N.

Donc on peut dire que N insertions est O(2N) donc O(N)

Par conséquent 1 insertion est O(1).

Donc c’est constant.

Le temps amorti de l’insertion d’un élément est O(1) pour ArrayList.

La série O(n) va continuer avec des clés de réussite, des questions exemplaires et leurs solutions.